How to scale a grid on a page for uniform margins?

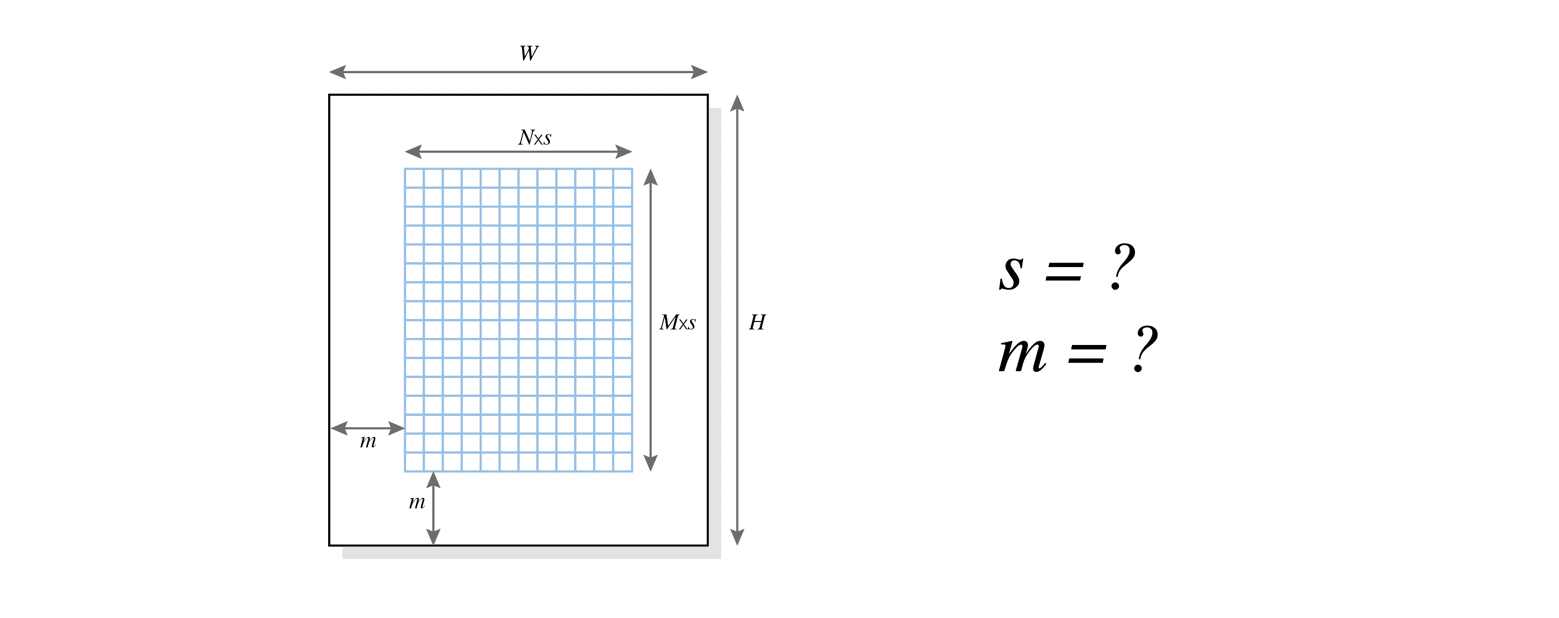
The problem

Several generative art algorithms, such as Truchet tiles, use a regular grid of square cells. For example, check this interactive demo from the Generative Design book or these few pieces of mine.

Now, let’s say you want to generate an iteration of your algorithm for printing or plotting such that all margins around the grid are the same for the given paper size. You can of course adjust the number of cell rows and columns, but how should you size the cell such as to achieve uniform margins?

The image above illustrates the problem. For a given page of size $W \times H$ and a regular grid of $N \times M$ cells, what should be the cell size $s$ to achieve uniform margins $m$ around the grid? What is then the value of $m$?

The solution

This is easy to solve with a bit of math. Here is the system of two equations that must be solved:

with all parameters ($N$, $M$, $W$, $H$) and the cell size $s$ being strictly positive.

Solving this for $m$ and $s$ is no rocket science but Wolfram Alpha can do the job for you if your high school math is rusty!

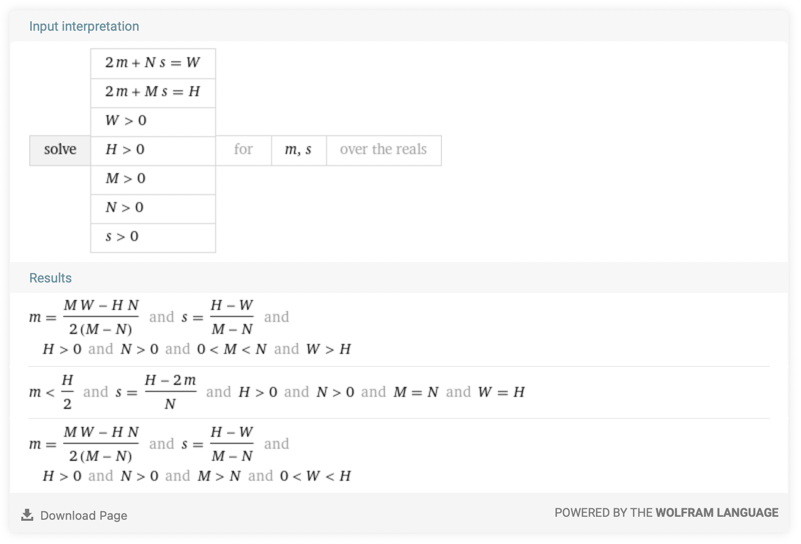
We have the following solutions:

The first solution corresponds to the special case of a square page size. In this case, the grid must be square ($N=M$) and the margins may have an arbitrary value, with the cell size varying accordingly. This is not very surprising.

The second solution is where things become interesting. As intuition dictates, it is valid only if the grid orientation (portrait or landscape) matches the paper orientation. If so, uniform margins is achieved by choosing a cell size of $s = \frac{H-W}{M-N}$.

Note that the resulting margin $m$ may, depending on the parameters, be negative. In this case, the grid overflows all around the page by a constant distance. This making plotting/printing your piece inconvenient, you will have to adjust $N$ and/or $M$ to reach a positive margin value.

The demo

I made a demonstration sketch made with vsketch. Here is how it looks:

This is a simplified version of the code which can be used as a starting point for your next grid-based design:

import itertools
import vsketch

class MySketch(vsketch.SketchClass):
    N = vsketch.Param(5, 1)
    M = vsketch.Param(7, 1)

    def draw(self, vsk: vsketch.Vsketch) -> None:
        vsk.size("a4", landscape=False, center=False)   # disable auto-centering

        cell_size = (vsk.height - vsk.width) / (self.M - self.N)
        margin = (self.M * vsk.width - self.N * vsk.height) / 2 / (self.M - self.N)
        
        if cell_size > 0:
            # account for the computed margin
            vsk.translate(margin, margin)
            
            # draw the grid
            for i, j in itertools.product(range(self.N + 1), range(self.M + 1)):
                vsk.point(i * cell_size, j * cell_size)
        else:
            # ERROR: N and M values must be adjusted!
            pass